Good Grigori

Grigori Perelman, a modern day Siddhartha?

There is much written and discussed about those who find fame in our current era. Indeed, there are numerous ways to earn your 15 minutes. Here are three that seem to be commonplace nowadays: through an aggregation of wealth, through questionable behavior, or by accomplishing things.

To me, the best, the most commendable, (or most good, to be in line with this substack’s theme, but grammatically lacking) is the third one.

So in today’s Good Thing, we are going to talk about a good Russian man who solved an insolvable problem and defines his life by a quest for truth and logic.

In 1966, St. Petersburg was still known as Leningrad. In that year, Grigori Perelman was born in Leningrad. Much like the Hungarian aliens, Al Teller or John Von Neumann, from an early age, Perelman’s proficiency at mathematics was apparent and celebrated. By the age of 10, his skills were so evident that his mother (more on her at the end) quit her job to ensure Grigori’s skills were maximized.

At the age of 15, Perelman won a gold medal and achieved a perfect score as part of the Soviet team competing the International Mathematical Olympiad, an international competition for high schoolers.

At 24, Perelman completed his Ph.D. at the School of Mathematics and Mechanics at Leningrad State University. He then tried positions at NYU, SUNY, and Berkeley before realizing: “I realize that in Russia I work better.”

He returned to St. Petersburg and landed at the Steklov Institute for a whole year before disappearing from the public and academic eye.

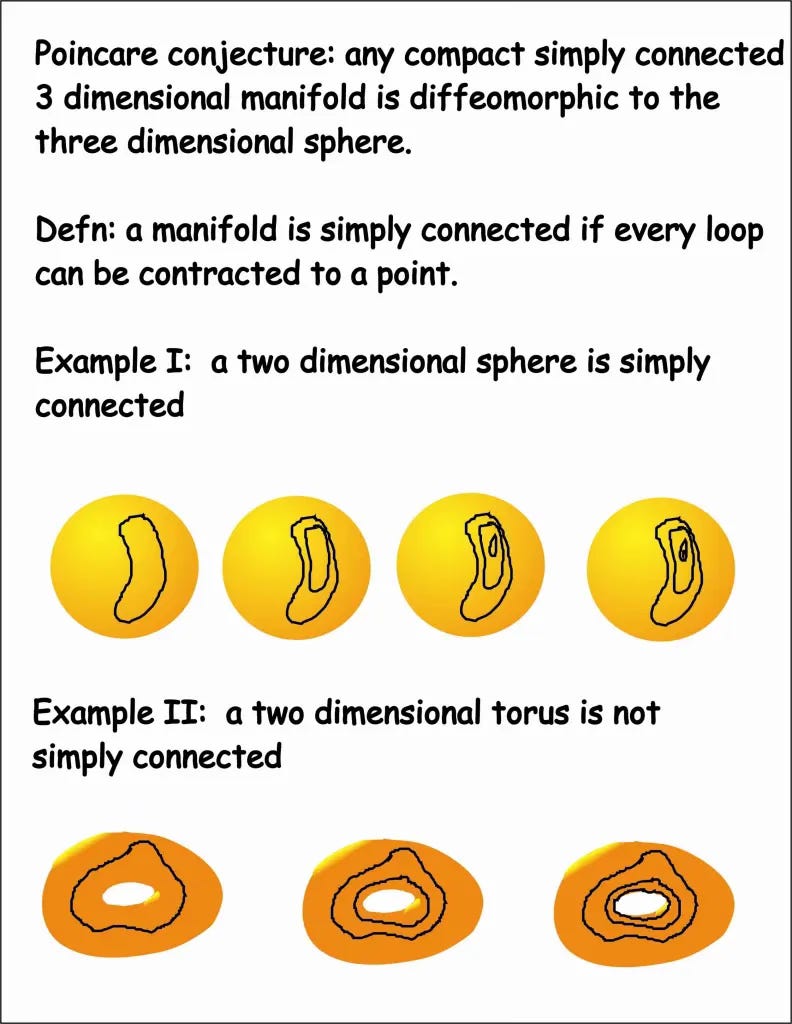
Then, in a triumvirate of papers posted to the website arXiv between November 2002 and July 2003, Perelman outlined a series of proofs that proved the Poincaré conjecture.

The Poincaré conjecture is a peculiar mathematical problem that I don’t fully understand myself. Attempts to explain it deal with spheres, donuts, and this peculiar trait called homeomorphism. Needless to say, some guy named Poincaré (French, late 1800s) posed it, and many people have tried to prove it.

And failed.

Now we have spoken on this Substack about prizes and how they can drive great achievement and innovation. Perelman’s solution is the ONLY solution found so far for the Millennium Prize Problems. Like any good prize, the Millennium Prizes come with an award of US$1,000,000 (1 mill.) BUT! When it came to claiming the reward for his solution, Perelman showed nothing but disinterest and maybe even disdain. He turned down the money, the Millennium Prize, and the Fields medal because…

"It was completely irrelevant for me ... everybody understood that if the proof is correct then no other recognition is needed."

Now, Perelman spends his time in a field picking mushrooms and looking after his mother on the outskirts of Saint Petersburg. Accolades, world fortune, and fame are of much less importance to Perelman than pursuing truth and clarity. It’s not quite Siddhartha at the river, but it’s a lovely story about personal passion being enough for one rather smart and good man.

In 2006, Sylvia Nasar (author of "A Beautiful Mind" about Nobel Prize-winning mathematician John Forbes Nash) and a colleague traveled to St. Petersburg and managed to track down Perelman. Perelman repeatedly said that he had retired from the mathematics community and no longer considered himself a professional mathematician.

The pair did run into a colleague of his, Mikhail Gromov, who gave us this banger quote:

“The ideal scientist does science and cares about nothing else.He [Perelman]”wants to live this ideal.”

Humility and idealism are a good match.